O ábaco é um antigo instrumento de
cálculo, que segundo muitos historiadores foi inventado na Mesopotâmia, pelo
menos em sua forma primitiva e depois os chineses e romanos o aperfeiçoaram. Uma variedade de ábacos foram desenvolvidos; o mais
popular utiliza uma combinação de dois números-base (2 e 5) para representar
números decimais.
O ábaco é um antigo instrumento de
cálculo, que segundo muitos historiadores foi inventado na Mesopotâmia, pelo
menos em sua forma primitiva e depois os chineses e romanos o aperfeiçoaram. Uma variedade de ábacos foram desenvolvidos; o mais
popular utiliza uma combinação de dois números-base (2 e 5) para representar
números decimais.
O primeiro ábaco foi quase de certeza construído
numa pedra lisa coberta por areia ou pó. Palavras e letras eram desenhadas na
areia; números eram eventualmente adicionados e bolas de pedra eram
utilizadas para ajuda nos cálculos. Os babilônios utilizavam este ábaco em
2700–2300 a.C. A origem do ábaco de contar com bastões é
obscuro, mas a Índia, a Mesopotâmia ou o Egito são vistos como prováveis pontos de
origem. A China desempenhou
um papel importante no desenvolvimento do ábaco.
Diferentes tipos de ábaco nas
diversas civilizações
Ábaco chinês
O registro mais antigo que se conhece
é um esboço presente num livro da dinastia Yuan (século XIV). O seu nome em
Mandarim é "Suan Pan" que significa "prato de cálculo". O
ábaco chinês tem 2 contas em cada vareta de cima e 5 nas varetas de baixo
razão pela qual este tipo de ábaco é referido como ábaco 2/5. O ábaco
2/5 sobreviveu sem qualquer alteração até 1850, altura em que aparece
o ábaco do tipo 1/5, mais fácil e rápido.Os modelos 1/5 são
raros hoje em dia, e os 2/5 são raros fora da China exceto nas suas comunidades
espalhadas pelo mundo.
Ábaco japonês
Por volta de 1600 D.C., os japoneses
adotaram uma evolução do ábaco chinês 1/5 e chamado de Soroban. O ábaco do tipo
1/4, o preferido e ainda hoje fabricado no Japão, surgiu por volta de
1930. Uma vez que os japoneses utilizam o sistema decimal optaram por
adaptar o ábaco 1/5 para o ábaco 1/4, desta forma é possível obter valores
entre 0 e 9 (10 valores possíveis) em cada coluna. O soroban passou
por significativas mudanças até ser obtida
a configuração atual. O instrumento de cálculo fora "importado" da
China há quase 380 anos, em 1622. Ao Brasil foi trazido pelos primeiros
imigrantes, em 1908, ainda em sua
versão antiga, mas já modificada do original chinês; em 1953 é introduzido o
soroban moderno, utilizado atualmente.
Ábaco Asteca
De acordo com investigações recentes,
o ábaco Asteca (Nepohualtzitzin), teria surgido entre 900-1000 D.C. As contas
eram feitas de grãos milho atravessados por cordéis montados numa armação de
madeira. Este ábaco é composto por 7 linhas e 13 colunas. Os números 7 e 13 são
números muito importantes na civilização asteca. O número 7 é sagrado, o número
13 corresponde à contagem do tempo em períodos de 13 dias.
Ábaco Russo
O ábaco russo, inventado no século
XVII, e ainda hoje em uso, é chamado de Schoty. Este ábaco opera de forma
ligeiramente diferente dos ábacos orientais. As contas movem-se da esquerda
para a direita e o seu desenho é baseado na fisionomia das mãos humanas.
Colocam-se ambas as mãos sobre o ábaco, as contas brancas correspondem aos polegares das mãos (os polegares devem estar
sobre estas contas) e as restantes contas movem-se com 4 ou 2 dedos.
Ábaco Grego
Uma tábua encontrada na ilha grega de
Salamina em 1846 data de 300 a.C. fazendo deste o mais velho ábaco descoberto
até agora. É um ábaco de mármore de 149 cm de comprimento, 75 cm de largura e
de 4,5 cm de espessura, no qual existem 5 grupos demarcações. No centro da
tábua existe um conjunto de 5 linhas paralelas igualmente divididas por uma
linha vertical, tampada por um semicírculo na intersecção da linha horizontal
mais ao canto e a linha vertical única. Debaixo destas linhas, existe um espaço
largo com um a rachadura horizontal a dividi-los. Abaixo desta rachadura, existe
outro grupo de onze linhas paralelas, divididas em duas secções por uma linha
perpendicular a elas, mas com o semicírculo no topo da intersecção; a terceira,
sexta e nona linhas estão marcadas com uma cruz onde se intersectam com a linha
vertical.
Ábaco Romano
O método normal de cálculo na Roma
antiga, assim como na Grécia antiga,era mover bolas de contagem numa tábua
própria para o efeito. As bolas de contagem originais denominavam-se calculi.
Mais tarde, e na Europa medieval, os jetons começaram a ser manufaturados.
Linhas marcadas indicavam unidades, meias dezenas, dezenas, etc., como na
numeração romana. O sistema de contagem contrária continuou até à queda de
Roma, assim como na Idade Média e até ao século XIX, embora já com uma
utilização mais limitada.
Versão moderna
de um ábaco.
Até hoje, os ábacos são fabricados e usados em
transações comerciais. Não só por tradição como também por ser um meio
altamente eficiente de executar operações matemáticas.
ATIVIDADE
PARA COMPREENSÃO DAS CASAS DECIMAIS COM O USO DO ÁBACO.
OBJETIVO:
Estimular
a criança a refletir sobre as posições dos números e a representação
numérica.
RECURSOS DIDÁTICOS:
Atividades
impressas e o ábaco.
METODOLOGIA:
Iniciar
as atividades explicando cada casa dezena, centena e unidade. Após colocar em
prática através de exercícios que utilizam o ábaco.
EXPLICAÇÃO DE COMO USAR
UM ABÁCO
Cada 10 unidades de uma ordem formam uma unidade da ordem
seguinte. Observe.
10 unidades = 1 dezena = 10
10 dezenas = 1 centena = 100
10 centenas = 1 unidade de milhar = 1000
Utilizando esse ábaco podemos explicar para as crianças:
Amarelo - é a casa das UNIDADES
Vermelho - é a casa das DEZENAS
Verde - é a casa das CENTENAS
Azul - é casa dos MILHARES.
Observando esse número: 151
O número 1 representa as UNIDADES, então na casinha amarela vai ficar 1
bolinha.E vale 1.
O número 5 representa as DEZENAS ,então na casinha vermelha vão ficar 5
bolinhas.Que vale 50
O número 1 representa as CENTENAS,então na casinha verde vai ficar 1
bolinha.Que vale 100,
ou seja 100+50+1= 151
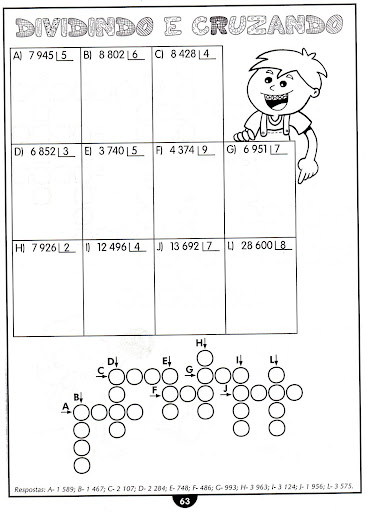
ATIVIDADES
1- A
ATIVIDADE PROPOSTA É SUGERIR OS NÚMEROS PARA AS CRIANÇAS, PARA QUE ELAS
COLOQUEM NO ÁBACO.
Exemplo:
Esse número tem 1 centena, 2 dezenas e 8 unidades.Que número é esse?
Conforme a criança for pegando o ritmo o professor vai colocando mais desafios.
2- ATIVIDADE
IMPRESSA
DEPOIMENTO
DA CRIANÇA USO DO ÁBACO.
A
atividade foi proposta a uma criança de 7 anos e meio que cursa o 2º ano do
ensino fundamental I, o mesmo relatou que não conhecia o ábaco, a criança
falou que era bom fazer com o ábaco porque dava para ver, tirar e colocar as
argolinhas do pauzinho e a matemática ficava mais fácil.
A
criança apresentou interação com o ábaco e compreensão das casas decimais, e a
mesma percebeu a possibilidade de fazer operações diferentes, pois ao terminar
as atividades propostas, brincou de subtrair tirando as peças e dizendo quanto
ficava e de adição onde colocava argolinhas e falava que tinha mais.

Idade das crianças: 09 anos Série: 5º
Ano (4ª Série)
Perfil do aluno: Os
alunos têm um conhecimento sobre cálculos básicos como subtração, adição,
divisão e multiplicação, já conhecem o ábaco das séries anteriores. Esperamos
dos alunos uma habilidade maior com o ábaco e que eles tenham um raciocínio
lógico diante das perguntas.
Entregaremos a cada criança
um ábaco e veremos a reação dela diante do objeto, após isso lançaremos os
desafios.
1) Qual a utilidade do ábaco? Após responder
faça duplas e demonstre a utilização dele nos primórdios, o porquê de este ser
tão útil antigamente.
R: Utilizamos o
ábaco para cálculos, foi muito importante antigamente pela inexistência de
calculadoras, se tornando uma forma rápida de fazer grandes cálculos, como por
exemplo, um pastor de ovelhas, para calcular quantas ovelhas tinha fazia os
cálculos com pedras, cada dez ovelhas contadas passava-se uma pedra de cor
diferente para outro circulo. (pode-se representar através da dinâmica entre as
duplas essa contagem).
2) Podemos construir um ábaco com
outros objetos? Se sim, de que maneira podemos fazer? Construa o ábaco em
duplas, da forma que acharem melhor.
R: Sim, podemos
construir com pedras, tampas, cordas, copos, entre outros objetos.
Construção do ábaco no chão
da sala de aula com cinco círculos desenhados utilizará as crianças para
representar as pedras, faremos a utilização apenas das unidades e dezenas;
3) Coloque nove dezenas, subtraia três dezenas, divida em dois. Qual é o
numero final?
R: 30
4) Coloque
uma dezena, divida em cinco partes. Quantas unidades ficaram em cada parte?
R: 2


.jpg)













.png)






.jpg)











.jpg)
.jpg)
.jpg)